3.5 Z-matrix Coordinates

Z-matrix notation is one of the most common molecular coordinate input forms. The Z-matrix defines the positions of atoms relative to previously defined atoms using a length, an angle and a dihedral angle. Again, note that all bond lengths and angles must be in Angstroms and degrees.

Note: As with the Cartesian coordinate input method, Q-Chem begins a calculation by taking the user-defined coordinates and translating and rotating them into a Standard Nuclear Orientation.

The first three atom entries of a Z-matrix are different from the subsequent entries. The first Z-matrix line declares a single atom. The second line of the Z-matrix input declares a second atom, refers to the first atom and gives the distance between them. The third line declares the third atom, refers to either the first or second atom, gives the distance between them, refers to the remaining atom and gives the angle between them. All subsequent entries begin with an atom declaration, a reference atom and a distance, a second reference atom and an angle, a third reference atom and a dihedral angle. This can be summarized as:

First atom.
Second atom, reference atom, distance.
Third atom, reference atom A, distance between A and the third atom, reference atom B, angle defined by atoms A, B and the third atom.
Fourth atom, reference atom A, distance, reference atom B, angle, reference atom C, dihedral angle (A, B, C and the fourth atom).
All subsequent atoms follow the same basic form as (4)

Example 3.8 Z-matrix for hydrogen peroxide

  O1
  O2   O1   oo
  H1   O1   ho   O2   hoo
  H2   O2   ho   O1   hoo   H1   hooh

Line 1 declares an oxygen atom (O1). Line 2 declares the second oxygen atom (O2), followed by a reference to the first atom (O1) and a distance between them denoted oo. Line 3 declares the first hydrogen atom (H1), indicates it is separated from the first oxygen atom (O1) by a distance HO and makes an angle with the second oxygen atom (O2) of hoo. Line 4 declares the fourth atom and the second hydrogen atom (H2), indicates it is separated from the second oxygen atom (O2) by a distance HO and makes an angle with the first oxygen atom (O1) of hoo and makes a dihedral angle with the first hydrogen atom (H1) of hooh.

Some further points to note are:

Atoms can be declared by either atomic number or symbol.
- If declared by atomic number, connectivity needs to be indicated by Z-matrix line number.
- If declared by atomic symbol either number similar atoms (e.g., H1, H2, O1, O2 etc.) and refer connectivity using this symbol, or indicate connectivity by the line number of the referred atom.
Bond lengths and angles can be entered either as variables/parameters or real numbers.
- Variables/parameters can be declared in any order.
- A single blank line separates parameters from the Z-matrix.

All the following examples are equivalent in the information forwarded to the Q-Chem program.

Example 3.9 Using parameters to define bond lengths and angles, and using numbered symbols to define atoms and indicate connectivity.

$molecule
   0 1
   O1
   O2  O1  oo
   H1  O1  ho  O2  hoo
   H2  O2  ho  O1  hoo  H1  hooh

   oo   =   1.5
   oh   =   1.0
   hoo  = 120.0
   hooh = 180.0
$end

Example 3.10 Not using parameters to define bond lengths and angles, and using numbered symbols to define atoms and indicate connectivity.

$molecule
   0 1
   O1
   O2  O1  1.5
   H1  O1  1.0  O2  120.0
   H2  O2  1.0  O1  120.0  H1  180.0
$end

Example 3.11 Using parameters to define bond lengths and angles, and referring to atom connectivities by line number.

$molecule
   0 1
   8
   8  1  oo
   1  1  ho  2  hoo
   1  2  ho  1  hoo  3  hooh

   oo   =   1.5
   oh   =   1.0
   hoo  = 120.0
   hooh = 180.0
$end

Example 3.12 Referring to atom connectivities by line number, and entering bond length and angles directly.

$molecule
  0 1
  8
  8  1  1.5
  1  1  1.0  2  120.0
  1  2  1.0  1  120.0  3  180.0
$end

Obviously, a number of the formats outlined above are less appealing to the eye and more difficult for us to interpret than the others, but each communicates exactly the same Z-matrix to the Q-Chem program.

3.5.1 Dummy Atoms

Dummy atoms are indicated by the identifier 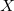$X$ and followed, if necessary, by an integer. (e.g., 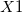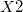$X1$ , $X2$ . Dummy atoms are often useful for molecules where symmetry axes and planes are not centered on a real atom, and have also been useful in the past for choosing variables for structure optimization and introducing symmetry constraints.

Note: Dummy atoms play no role in the quantum mechanical calculation, and are used merely for convenience in specifying other atomic positions or geometric variables.